Understanding learning with errors
Cryptographic protocols that perform computations on encrypted data without decrypting it are known as homomorphic encryption. Fully homomorphic encryption (FHE) protocols, systems which support arbitrary computations, often rely on different primitives than conventional cryptography systems. Most FHE systems in practice used lattice-based cryptography, relying on a computational hardness assumption known as the learning with errors (LWE) problem.
Cryptograhy relies on assumptions
Prior to the 20th century, cryptography did not rely on a formalized system of provable security. Rather, one set of people (cryptographers) would come up with clever ciphers, and another set of people (cryptanalysts) would attempt to break those ciphers. Encryption schemes such as the Caesar cipher, the Vingenère cipher, the Enigma, and other systems were not formally proven secure by cryptographers. Rather, they relied on obfuscation and statistical properties that made deciphering messages fairly difficult. However, each one of these systems had some sort of flaw that cryptanalysts were able to exploit to decipher encrypted messages. 1
Modern cryptography, starting in the 1970s and 80s, changed the way we define security to be about adversarial capabilities rather than strategies. Instead of attempting to figure out the many ways a potential adversary could attack a specific protocol, cryptographers base security protocols on well-studied problems for which no known solution exists. The fundamental assumption that much of cryptography rests on is that $P \neq NP$.
Why is this a bedrock assumption for many protocols? The definitions that cryptography uses today all come from security games, where an arbitrary distinguisher (the adversary) tries to figure out what the challenger (the protocol) is doing. For example, in the adversarial game below, the adversary $\mathcal{A}$ is trying to distinguish whether the challenger is providing it with either a pseudorandom bit string (Experiment 0) or a completely random string (Experiment 1).
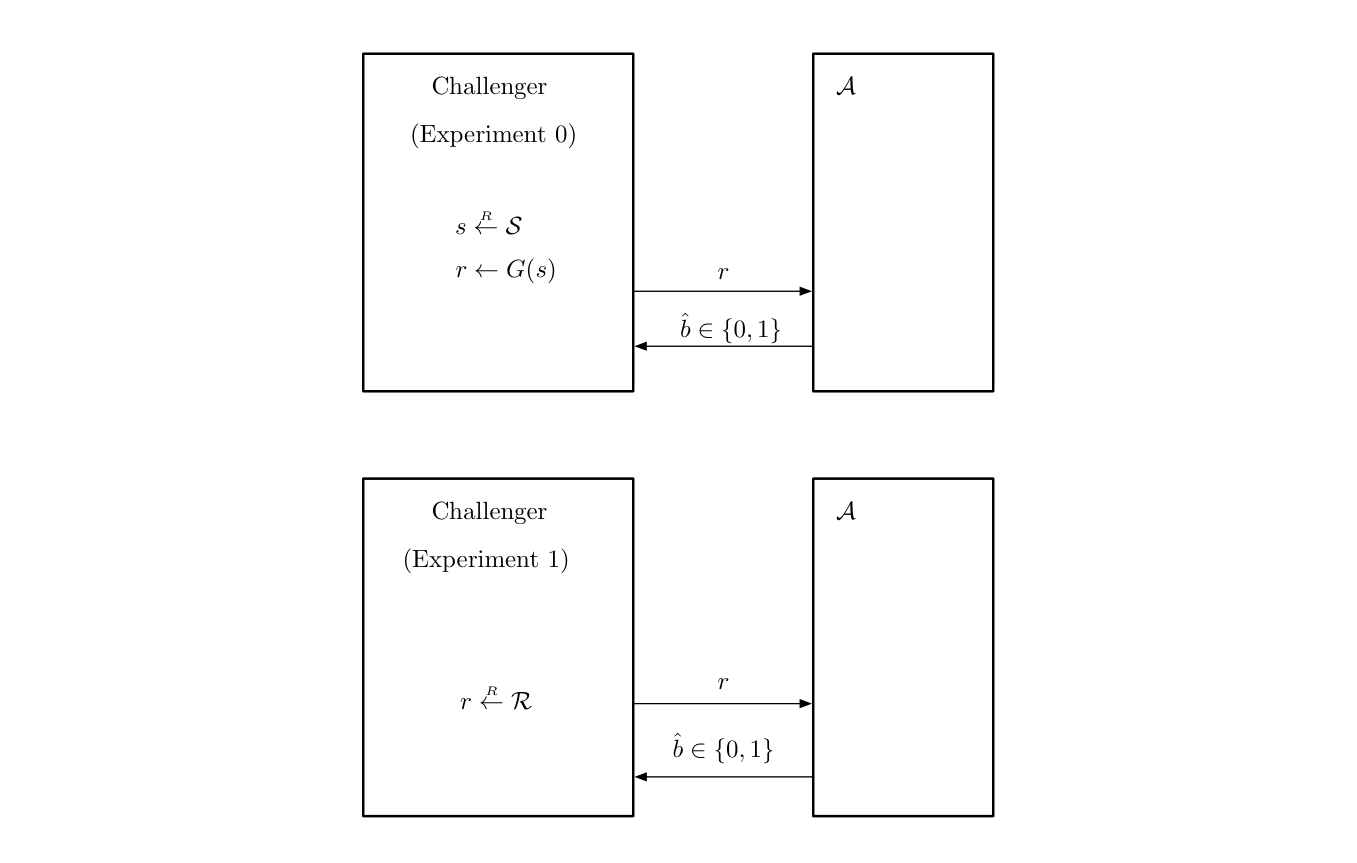
Source: "A Graduate Course in Applied Cryptography", Boneh and Shoup
The question of whether an adversary can distinguish between two games (or experiments, or scenarios) is a question that belongs to the complexity class NP. It can be verified by a deterministic machine (the algorithm used to create whatever artifact is being tested, e.g. a pseudorandom generator or encryption algorithm) and can be solved by a nondeterministic Turing machine. However, if there exists a deterministic Turing machine that can solve this question of distinguishability, then no cryptographic protocol relying on this model is secure.
This presents a benefit to cryptographers in both cases: either protocols that rely on this assumption are secure, or we will have an incredible breakthrough in mathematics.
Other assumptions
However, to build specific protocols, we often require more assumptions than this. The first two assumptions used to build secure protocols, the discrete log problem and the factoring problem, come from number theory.
Discrete Log
The discrete logarithm problem typically used in cryptography can be expressed as follows. Let $p$ be a prime number, and take the group $\mathbb{Z}_p^*$, the multiplicative group of numbers modulo $p$. Let $g \in \mathbb{Z}_p^*$ be a generator of the group $\mathbb{Z}_p^*$. Since $g$ is a generator, we can raise $g$ to the power of any element in $\mathbb{Z}_p^*$ and get a unique element from $\mathbb{Z}_p^*$ - a bijection.
Now, randomly select an element $x$ from $\mathbb{Z}_p^*$ and calculate $g^x = t$. The discrete log question is: given $t$, can you calculate $x$? The assumption that is relevant to cryptography is that it is computationally hard to find $x$ given $t$. 2 This assumption can be generalized to other groups outside of multiplicative modular integer sets, such as elliptic curve groups that are widely used today.
The first public protocol to use the discrete log assumption was Diffie-Hellman key exchange. Others, such as ElGamal and Schnorr, were developed using this assumption as their basis, and many systems today (DSA, TLS, SSH, PGP, Tor) have some form of the discrete log assumption guaranteeing their security.
Factoring and the RSA assumption
Suppose we have a number $N$ and two primes $p$ and $q$ such that $N = pq$. The factoring assumption states that given $N$, it is computationally hard to obtain $p$ and $q$. Intuitively, factoring a large composite number into two slightly less large primes appears to be a difficult problem. The fastest known factoring algorithm on a current computer is the general number field sieve (GNFS), which runs in sub-exponential time (not poly time).
The RSA assumption is slightly different: we take our numbers from before ($N$, $p$, and $q$) and select at random an exponent $e$ from $\mathbb{Z}_{\varphi(N)}$, where $\varphi(N) = (p-1)(q-1)$ is Euler’s totient function on $N$. We then select $x$ from $\mathbb{Z}_{N}^*$ and compute $y = x^e$. The RSA assumption states that given $N, y$ and $e$, it is computationally hard to determine $x$. This assumption comes directly from the RSA protocol itself. 3
Lattice-based cryptography
In 1994, Peter Shor invented a quantum algorithm (known as Shor’s algorithm) that is able to find the prime factors of an integer. The paper also states a similar algorithm that is able to compute discrete logs. This algorithm runs in polynomial time on a quantum computer, meaning that all protocols based on either the discrete log or the integer factoring assumptions are not secure against quantum computers.
Over the resulting decades, cryptographers have taken into account this new threat and started looking for computational hardness assumptions that would be resistant to quantum algorithms. One of the places where they looked was lattice theory.
Lattices
Lattice theory is at the intersection of abstract algebra and order theory. Formally, a lattice is defined as a partially ordered set in which each two-element subset has both a least upper bound and a greatest lower bound. 4 Lattices in $\mathbb{R}^n$ are a subset of this definition. They can be thought of what results from a change of basis in linear algebra. If you take all integer combinations of a basis for $\mathbb{R}^n$, you will then have a lattice.
Source: Wikimedia
While there are many interesting properties of lattices, a question relevant to computer science is whether there are problems that are computationally hard to perform. Such a computation would provide security against adversaries, who would be unable to perform such a computation given restrictions on their computational power.
The shortest vector problem is one such question. The problem is: given a basis $B$ of a lattice $L$ (the vector space $V$), what is the shortest non-zero vector, as measured by its Euclidean norm $||\mathbf{v}||_2$? 5 In other words: suppose I give you a set of vectors $\mathbf{v}_1, \mathbf{v}_2, …, \mathbf{v}_n$. These form a basis for some vector space (a lattice): you can take integer linear combinations (for example, $2\mathbf{v}_1 + 5\mathbf{v}_2 + …$) of them to obtain infinitely many points in the space. How would you find the shortest possible vector $\mathbf{v}$ in that space, such that $||\mathbf{v}||_2 = \underset{\mathbf{v} \in L \smallsetminus {0}}{\min} ||\mathbf{v}||_2$?

Source: Wikimedia
SVP is known to be NP-hard for randomized reductions. 6 Other questions, such as the gap shortest vector problem (GapSVP), shortest independent vector problem (SIVP), closest vector problem (CVP), and more also exist and provide computational hardness in different ways.
Computational hardness of lattice problems
One important property of lattice problems that makes them useful in cryptography is that their worst-case computational hardness is often equal to their average-case hardness. Proofs of this began with Ajtai’s papers in 1994 and 1996 on generating hard instances of lattice problems and the computational hardness of SVP. 7
Worst-case computational hardness refers to how difficult it is to compute a problem in the worst case possible. However, cryptography relies on average-case hardness. Each use of a cryptographic system must be difficult, not just the worst case of that system. These systems often rely on randomness to generate specific instances of a protocol (e.g., generate keys to use for encryption), and randomness pertains to a randomly selected, i.e. average case.
Equivalence between worst-case and average-case problems is crucial for lattice-based cryptography. It means that given a single instance of a lattice problem that is hard to solve, we can generate many equally hard instances of that problem. This allows for stronger guarantees around computational hardness in a variety of cases involving randomization.
LWE
One way to measure the usefulness of an assumption is by its complexity. The shortest vector problem is one such instance: it is simple to state, and fairly easy to understand. However, this is not the only measure of an assumption: one can also look at how long the problem has remained unsolved for, how much effort has been expended trying to solve it, and how useful or practical it is. SVP is useful across most of these metrics, but another problem has proven more flexible when designing new systems and protocols.
The learning with errors problem (LWE) can be stated somewhat precisely as follows. Fix a size parameter $n \geq 1$, a modulus $q \geq 2$, and an error probability distribution $\chi$ on $\mathbb{Z}_q$, the integers modulo $q$. We can define $A_{\mathbf{s}, \chi} \in \mathbb{Z}_q^n \times \mathbb{Z}_q$ as the probability distribution that is obtained by choosing a vecor $\mathbf{a} \in \mathbb{Z}_q^n$ uniformly at random, choosing $e$ in $\mathbb{Z}_q$ based on its probability distribution $\chi$, and computing the tuple $(\mathbf{a}, \langle \mathbf{a}, \mathbf{s} \rangle + e)$. Now: given $n, q, \chi$, and an arbitrary number of samples from the distribution $A_{\mathbf{s}, \chi}$, what is $\mathbf{s}$.
To convert this to an adversarial game (and a distinguishability problem), we can express the vectors $\mathbf{a}_1 … \mathbf{a}_n$ as a matrix $A$, and have a challenger select either a random vector $\mathbf{r} \stackrel{R}{\leftarrow} \mathbb{Z}_q^n$ and compute $A\mathbf{r}$, or select a secret $\mathbf{s}$ and an error vector $\mathbf{e} \leftarrow \mathbb{Z}_q^n$ based on $\chi$, and compute $A\mathbf{s} + \mathbf{e}$. The problem in this form is to distinguish between these two games, and the assumption is that they are computationally indistinugashable.
$$ \begin{aligned} A\mathbf{s} + \mathbf{e} \approx A\mathbf{r} \ \end{aligned} $$
The two paragraphs above may not make much sense at first, so let’s look at an example. This specific example was taken from a survey paper, “The Learning with Errors Problem”, by Oded Regev, the person who first came up with LWE (and later won the Gödel prize).
An example of learning with errors
First, we fix our parameters. For this example, $n = 4$ and $q = 17$. One way to think about “an arbitrary number of samples” from $A_{\mathbf{s}, \chi}$ is as a system of equations. In each equation, we will have 4 variables $(n = 4)$, all expressed modulo $17$. The coefficients of each variable can be expressed by the vector $\mathbf{a}$, whose entries we select uniformly at random from $\mathbb{Z}_q$. Let us forget about the error term $e$ for the moment and focus on the problem at hand.
Let’s sample $\mathbf{a} \hspace{0.25em} 6$ times, multiply it by the secret vector $\mathbf{s}$, and look at its result (the second element of the tuple given to us, denoted here as $c_i$). We might expect something like the following:
$$ \begin{aligned} 14s_1 + 15s_2 + 5s_3 + 2s_4 &= c_1 \: (\text{mod} \; 17) \\ 13s_1 + 14s_2 + 14s_3 + 6s_4 &= c_2 \: (\text{mod} \; 17) \\ 6s_1 + 10s_2 + 13s_3 + 1s_4 &= c_3 \: (\text{mod} \; 17) \\ 10s_1 + 4s_2 + 12s_3 + 16s_4 &= c_4 \: (\text{mod} \; 17) \\ 9s_1 + 5s_2 + 9s_3 + 6s_4 &= c_5 \: (\text{mod} \; 17) \\ 3s_1 + 6s_2 + 4s_3 + 5s_4 &= c_6 \: (\text{mod} \; 17) \\ \end{aligned} $$
How would you solve for $\mathbf{s}$, given the vector $\mathbf{c}$? The straightforward approach is to use Gaussian elimination. The brilliance of LWE, and what makes it computationally hard, is the error term $e$ for each equation.
Recall the second term of our tuple: $\langle \mathbf{a}, \mathbf{s} \rangle + e$. Suppose now that, instead of just presenting $c_1 … c_6$, I instead added an error term to each equation, where $e_i \stackrel{R}{\leftarrow} \{-1, 0, 1\}$ uniformly at random:
$$ \begin{aligned} 14s_1 + 15s_2 + 5s_3 + 2s_4 &\approx 8 &&(\text{mod} \; 17) \\ 13s_1 + 14s_2 + 14s_3 + 6s_4 &\approx 16 &&(\text{mod} \; 17) \\ 6s_1 + 10s_2 + 13s_3 + 1s_4 &\approx 3 &&(\text{mod} \; 17) \\ 10s_1 + 4s_2 + 12s_3 + 16s_4 &\approx 12 &&(\text{mod} \; 17) \\ 9s_1 + 5s_2 + 9s_3 + 6s_4 &\approx 9 &&(\text{mod} \; 17) \\ 3s_1 + 6s_2 + 4s_3 + 5s_4 &\approx 16 &&(\text{mod} \; 17) \\ \end{aligned} $$
We might try our first approach: Gaussian elimination. However, consider that each of our equations now has some error to it. The first equation could be $8$… or $7$… or $9$. We don’t know for cerain. If we guess the error term incorrectly (here, the probability of this is $\frac{2}{3}$), we’re in trouble - our error will compound throughout each equation. Since we have only 4 variables to solve for, we can limit this by taking the first four equations, but the probability that we are correct with every error term $e_i$ that we choose is $(1 - \frac{2}{3})^4$, and thus the probability that we are wrong somewhere is $1 - (1 - \frac{2}{3})^4 = \frac{80}{81}$. 8
This is the trickiness of the learning with errors problem - the errors in each term compound as we solve for $\mathbf{s}$, and they compound exponenetially. The best known algorithms for LWE run in exponential time, and there is evidence to suggest that quantum algorithms and tricks will not help to solve this problem - in some cases, they might increase the complexity. 9
Computational hardness
Regev [Reg05] and Chris Peikert [Pei09] established the hardness of the learning with errors problem by connecting it with two of the problems mentioned (but not described) above: GapSVP and SIVP. The core of Regev’s proof is a connection between LWE and SIVP: that is, given oracle access to solutions of the learning with errors problem, one is able to solve a worst-case lattice problem that we only know how to solve in exponential time. This problem can be stated as follows (from [Reg05]):
Let $q \geq 2$ be an integer and $\alpha$ be a real number in $(0, 1)$. Assume we are given access to an oracle that solves the $\text{LWE}$ problem with modulus $q$ and error parameter $\alpha$. Then, given as input any lattice $\Lambda$, a large enough polynomial number of samples from the discrete Gaussian distribution $D_{\Lambda^*, r}$, for some (not too small) $r$, and a point $\mathbf{x}$ witin distance $\alpha q / (\sqrt{2r})$ of $\Lambda$, we can output the (unique) closest lattice point $\mathbf{x}$ in polynomial time.
Note that the radius does not depend on $n$ but only on $q$, $\alpha$, and $r$. This solves the lattice problem BDD (bounded distance decoding), another lattice problem focused on decoding a lattice. 10 This problem can be stated in terms of GapSVP, as Peikert showed in 2009. Regev, in his original proof, combined the proposition above with a quantum procedure (creating a periodic Gaussian distribution) to reduce the problem to the shortest independent vector problem (SIVP) and GapSVP.
Related problems
The learning with errors problem is very versatile, but computationally expensive. The size of the matrix $A$ required for the protocol is on the order of $n^2$, as you need at least that many vectors to decode $\mathbf{s}$, and often has $m > n$ columns (a short, fat matrix). It is much more desirable to have key sizes on the order of $O(n)$, as it makes practical usage of a cryptographic protocol easier.
Ring-LWE allows us to replace the group $\mathbb{Z}_q^n$ with the ring $\mathbb{Z}_q[x] / \langle x^n + 1 \rangle$. The idea is to assume structure in the LWE samples ($A$) provided, and to condense this representation. We assume $n$ is a power of two and select the first vector of $A$ $\mathbf{a}_1 = (a_1, a_2, … a_n)$ as before, uniformly at random from $\mathbb{Z}_q^n$. We then replace the remaining vectors $(\mathbf{a}_{2} … \mathbf{a}_n)$ with $\mathbf{a}_i = (\mathbf{a}_i, … \mathbf{a}_n, -\mathbf{a}_1 … -\mathbf{a}_{i-1})$. These permutations give a ring structure, which is why we must have $n$ as a power of two (to guarantee that we cannot reduce $x^n + 1$ over $\mathbb{Q}$ by factoring it). These remaining vectors now only require $O(n)$ storage (we are repeating elements from $a_1$) and we can speed up vector operations using the fast Fourier transform. (e.g., convert polynomials to point-value representation, multiply, and convert back in O(n log n) rather than O(n^2)).
A dual problem with LWE is known as the short integer solutions problem (SIS). In this lattice problem, we are given vectors $\mathbf{a}_1, \mathbf{a}_2, …$ selected uniformly at random from $\mathbb{Z}_q^n$ and have to determine a “small” linear combination $\mathbf{s} = c_1 \mathbf{a}_1 + c_2 \mathbf{a}_2 + …$ such that $\displaystyle\sum_{i=1}^n \mathbf{a}_i + \mathbf{s} = 0$.
Crypto uses
Though the purpose of this post is primarily to go over the learning with errors assumption and its computational hardness, it is important to mention some of the cryptographic protocols based off of it.
Public key protocols: Regev encryption [Reg05] was the first to use the LWE assumption as the basis for a public key cryptography system. It used the random matrix $A \in \mathbb{Z}_q^{n\times m}$ and random vector $\mathbf{b} \in \mathbb{Z}_q^m$ as its public key and the vector $\mathbf{s} \in \mathbb{Z}_q^m$ as its secret key. To encrypt a message $m$, the protocol goes bit by bit. For a given bit $x$, you select a random vector $\mathbf{r} \in \mathbb{Z}_q^n$ and compute $(A\mathbf{r}, \mathbf{b}'\mathbf{r} + x\lfloor \frac{q}{2} \rfloor) = (c_1, c_2)$, To decrypt, calculate $\hat{x} = c_2 - \mathbf{s}' c_1$. If closer to $\lfloor \frac{q}{2} \rfloor$ modulo $q$, output 1, else ouptut 0.
Other public key protocols using LWE (or ring-LWE) include NTRU Prime and SABER.
FHE protocols: The first fully homomorphic encryption scheme was created by Craig Gentry in his PhD thesis from 2009. It was later improved upon in the GSW scheme, which simplified the construction of FHE and reduced the growth of noise between computations.
NIST standards: Last month, the National Institute of Standard and Technology released its first set of finalized post-quantum protocols. Two of the protocols, Kyber and Dilithium, both come from the Cryptographic Suite for Algebraic Lattices (CRYSTALS). Both rely on variants of the LWE assumption, modular LWE (MLWE).
References
There are many excellent resuoreces online. The primary ones I used in this post were Vinod Vaikuntanathan’s notes on lattices and Oded Regev’s survey of LWE. For a survey of cryptographic assumptions, see Goldwasser and Kalai’s position paper. Others included the various papers cited throughout the post and in the footnotes, as well as Wikipedia. For foundational crypography concepts, I used Boneh and Shoup’s A Graduate Course in Applied Cryptography - I took no specific definitions from the book, but my education on modern cryptographic primitives came from its chapters. I highly recommend if you are interested in understanding cryptographpy at more than a surface level. Any errors in conveying their definitions and explantions of concepts are mine.
-
See Daniel Kahn’s excellent book, The Codebreakers, for more on the history of early ciphers (and the field of cryptography). ↩︎
-
In case it is unclear, it is assumed that in addition to the number $t$, the group $G$ and the generator $g$ are also public information. The deeper principle behind this (and modern cryptography more generally) is known as Kerckhoff’s Principle: the security of a cryptosystem must lie in the choice of its keys only, and everything else (including the algorithm itself) should be considered public knowledge. ↩︎
-
To learn more about RSA, read the original paper or consult the Internet (or your LLM of choice). ↩︎
-
This comes from the Encyclopedia of Mathematic’s definition of a lattice. For more on lattice theory, J.B. Nation has very helpful introductory notes to the subject. ↩︎
-
Here, we will assume use of the Euclidean norm, but note that any norm of your choosing will work here. ↩︎
-
See this paper by Ajtai for the proof of this statement, as well as an explanation of the term “randomized reduction” in the first section. ↩︎
-
The above footnote contains the 1996 paper; here is a link to his paper from 1994. The paper explains how to generate average-case hardness from worst-case hardness. ↩︎
-
In this case, $\mathbf{s} = (0,13,9,11)$ ↩︎
-
See this episode of the “Security Cryptography Whatever” podcast for an explanation by Martin Albrecht about why this might be the case (timestamp: 22:10, go further back for context on the algorithms used) ↩︎
-
For more on BDD and its computational hardness, see this paper by Bennett and Peikert ↩︎